Quantum Teleportation¶
Quantum teleportation allows two parties that share an entangled pair to transfer an arbitrary quantum state using only classical communication. This process has tremendous applicability to quantum networks, transferring fragile quantum states between distant nodes. Conceptually, quantum teleportation is the inverse of superdense coding.
In general, all quantum teleportation experiments have the same underlying structure. Two distant parties, Alice and Bob, are connected via a classical information channel and share a maximally entangled state. Alice has an unknown state \(|\psi\rangle\) which she wishes to send to Bob. She performs a joint projective measurement of her state and her half of the entangled state and communicates the outcomes to Bob, who operates on his half of the entangled state accordingly to reconstruct \(|\psi\rangle\).
The source code for this demo is included in the demos directory of the SQUANCH repository.
Protocol¶
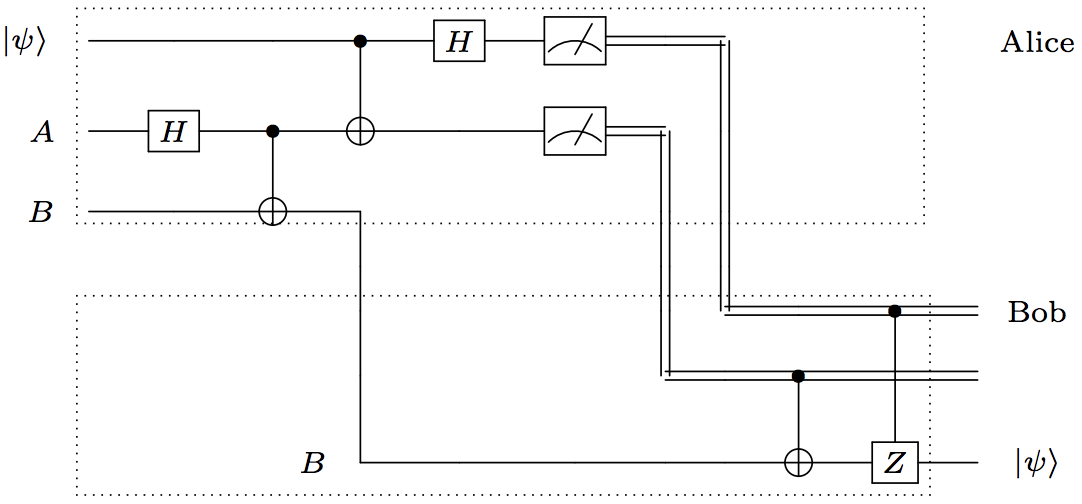
In this demo, we’ll implement a simple two-party quantum teleportation protocol using the above circuit diagram.
- Alice generates an entangled two-particle state \(\lvert AB \rangle = \frac{1}{\sqrt{2}} \left (\lvert 00 \rangle + \lvert 11 \rangle \right )\), keeping half of the state and sending the other half to Bob.
- Alice entangles her qubit \(|\psi\rangle\) with her ancilla \(A\) by applying controlled-not and Hadamard operators.
- Alice jointly measures \(|\psi\rangle\) and \(A\) and communicates the outcomes to Bob through a classical channel. Bob’s qubit is now in one of four possible Bell states, one of which is \(|\psi\rangle\), and he will use Alice’s two bits to recover \(|\psi\rangle\)
- Bob applies a Pauli-X operator to his qubit if Alice’s ancilla collapsed to \(\lvert A \rangle \mapsto \lvert 1 \rangle\), and he applies a Pauli-Z operator to his qubit if her qubit collapsed to \(\lvert \psi \rangle \mapsto \lvert 1 \rangle\). He has thus transformed \(|B\rangle \mapsto |\psi\rangle\).
Implementation¶
Quantum teleportation is a simple protocol to implement in any quantum computing simulation framework, but SQUANCH’s Agent and Channel modules provide an intuitive way to work with sending and receiving qubits, and the QStream module allows you to create performant simulations of teleporting a large number of states in succession.
First, let’s import what we’ll need.
import numpy as np
import matplotlib.pyplot as plt
from squanch import *
Now, we’ll want to define the behavior of Alice and Bob. We’ll extend the Agent class to create two child classes, and then we can change the run() method for each of them. For Alice, we’ll want to include logic for creating an EPR pair and sending it to Bob, as well as the subsequent entanglement and measurement logic.
class Alice(Agent):
'''Alice sends qubits to Bob using a shared Bell pair'''
def distribute_bell_pair(self, a, b):
# Create a Bell pair and send one particle to Bob
H(a)
CNOT(a, b)
self.qsend(bob, b)
def teleport(self, q, a):
# Perform the teleportation
CNOT(q, a)
H(q)
# Tell Bob whether to apply Pauli-X and -Z over classical channel
bob_should_apply_x = a.measure() # if Bob should apply X
bob_should_apply_z = q.measure() # if Bob should apply Z
self.csend(bob, [bob_should_apply_x, bob_should_apply_z])
def run(self):
for qsystem in self.qstream:
q, a, b = qsystem.qubits # q is state to teleport, a and b are Bell pair
self.distribute_bell_pair(a, b)
self.teleport(q, a)
Note that you can add arbitrary methods, such as distribute_bellPair() and teleport(), to agent child classes; just be careful not to overwrite any existing class methods other than run().
For Bob, we’ll want to include the logic to receive the particle from Alice and act on it according to Alice’s measurement results.
class Bob(Agent):
'''Bob receives qubits from Alice and measures the results'''
def run(self):
measurement_results = []
for _ in self.qstream:
# Bob receives a qubit from Alice
b = self.qrecv(alice)
# Bob receives classical instructions from alice
should_apply_x, should_apply_z = self.crecv(alice)
if should_apply_x: X(b)
if should_apply_z: Z(b)
# Measure the output state
measurement_results.append(b.measure())
# Put results in output object
self.output(measurement_results)
Now we want to prepare a set of states for Alice to teleport to Bob. Since each trial requires a set of three qubits, we’ll allocate space for a \(3 \times 10\) QStream. We’ll encode the message as spin eigenstates in the QStream:
# Prepare the initial states
qstream = QStream(3,10) # 3 qubits per trial, 10 trials
states_to_teleport = [1, 0, 1, 0, 1, 0, 1, 0, 1, 0]
for state, qsystem in zip(states_to_teleport, qstream):
q = qsystem.qubit(0)
if state == 1: X(q) # flip the qubits corresponding to 1 states
Now let’s make the agent instances. We create a shared output dictionary to allow agents to communicate between processes. Explicitly allocating and passing an output object to agents is necessary because each agent spawns and runs in a separate process, which (generally) have separate memory pools. (See Agent API for more details.) For agents to communicate with each other, they must be connected via quantum or classical channels. The Agent.qconnect and Agent.cconnect methods add a bidirectional quantum or classical channel, repsectively, to two agent instances and take a channel model and kwargs as optional arguments. In this example, we won’t worry about a channel model and will just use the default QChannel and CChannel options. Let’s create instances for Alice and Bob and connect them appropriately
# Make and connect the agents
out = Agent.shared_output()
alice = Alice(qstream, out)
bob = Bob(qstream, out)
alice.qconnect(bob) # add a quantum channel
alice.cconnect(bob) # add a classical channel
Finally, we call agent.start() for each agent to signal the process to start running, and agent.join() to wait for all agents to finish before proceeding in the program.
# Run everything
alice.start()
bob.start()
alice.join()
bob.join()
print("Teleported states {}".format(states_to_teleport))
print("Received states {}".format(out["Bob"]))
Running what we have so far produces the following output:
Teleported states [1, 0, 1, 0, 1, 0, 1, 0, 1, 0]
Received states [1, 0, 1, 0, 1, 0, 1, 0, 1, 0]
So at least for the simple cases, our implementation seems to be working! Let’s do a little more complex test case now.
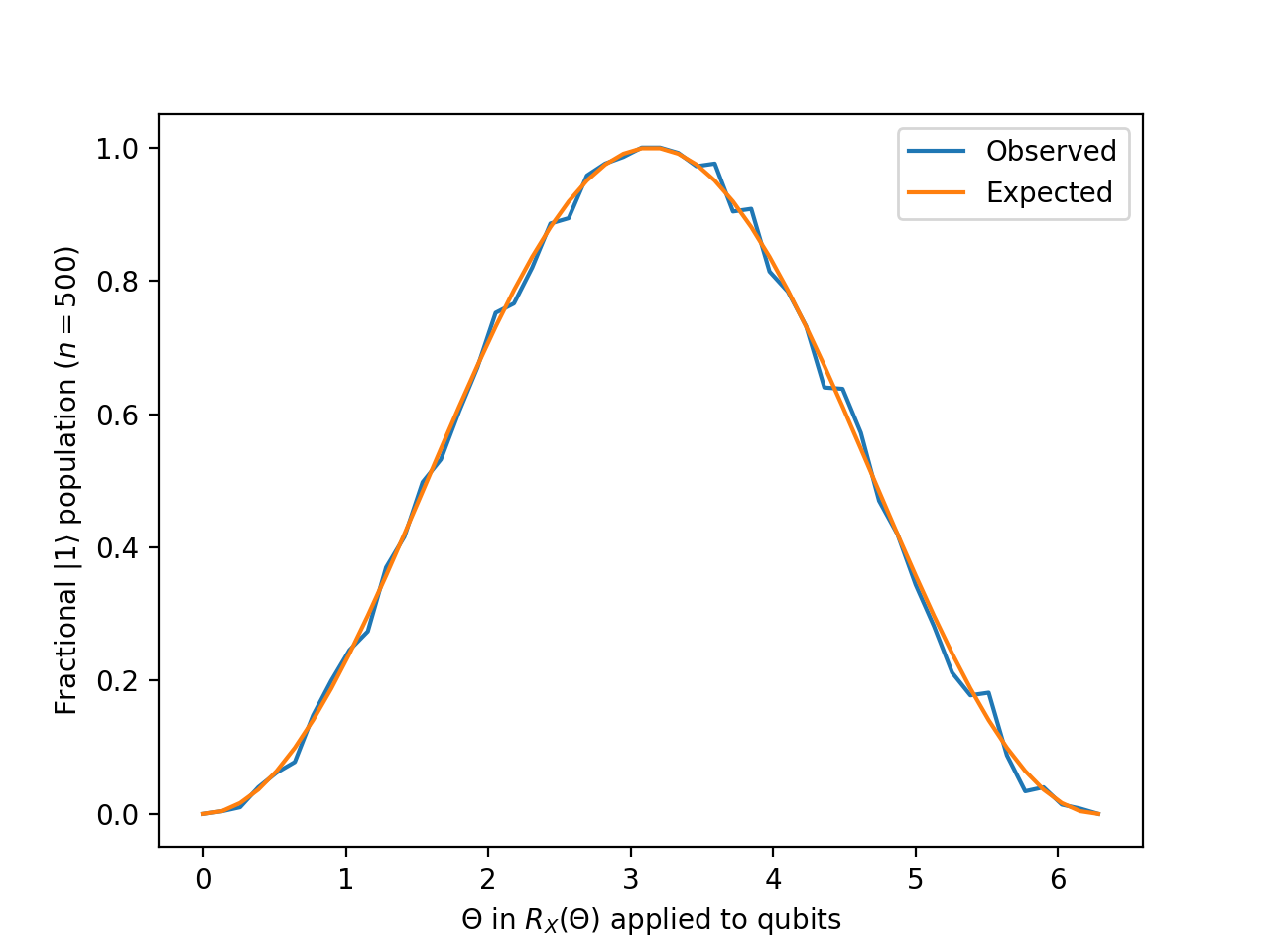
We’ll now try teleporting an ensemble of identical states \(R_{X}(\theta) \lvert 0 \rangle\) for several values of \(\theta\). We’ll then measure each teleported state and see how it compares with the expected outcome.
angles = np.linspace(0, 2 * np.pi, 50) # RX angles to apply
num_trials = 250 # number of trials for each angle
# Prepare the initial states in the stream
qstream = QStream(3, len(angles) * num_trials)
for angle in angles:
for _ in range(num_trials):
q, _, _ = qstream.next().qubits
RX(q, angle)
# Make the agents and connect with quantum and classical channels
out = Agent.shared_output()
alice = Alice(qstream, out = out)
bob = Bob(qstream, out = out)
alice.qconnect(bob)
alice.cconnect(bob)
# Run the simulation
Simulation(alice, bob).run()
# Plot the results
results = np.array(out["Bob"]).reshape((len(angles), num_trials))
observed = np.mean(results, axis = 1)
expected = np.sin(angles / 2) ** 2
plt.plot(angles, observed, label = 'Observed')
plt.plot(angles, expected, label = 'Expected')
plt.legend()
plt.xlabel("$\Theta$ in $R_X(\Theta)$ applied to qubits")
plt.ylabel("Fractional $\left | 1 \\right >$ population")
plt.show()
This gives us the following pretty plot.
Source code¶
The full source code for this demonstration is available in the demos directory of the SQUANCH repository.