Superdense Coding¶
Superdense coding is a method to deliver any two classical bits using a single quantum bit. The protocol allows two agents, Alice and Bob, to use an entangled bell state pair along with interaction with a single qubit to transmit two classical bits of information.
This protocol enables quantum computers to interact as a network in sharing classical information using qubits. Superdense coding transports two classical bits by sending a qubits, and thus is the inverse of quantum teleportation.
Protocol¶
Superdense Coding involves three agents, Alice, Bob, and Charlie. Charlie prepares the bell state pair and distributes the entangled qubits to Alice and Bob. Alice operates on her bell state pair from Charlie based on the classical bits she wishes to send to Bob, and then sends her bell state pair to Bob. Finally, Bob switches back into a computational basis and measures each qubit to recreate Alice’s classical bits.
Circuit¶
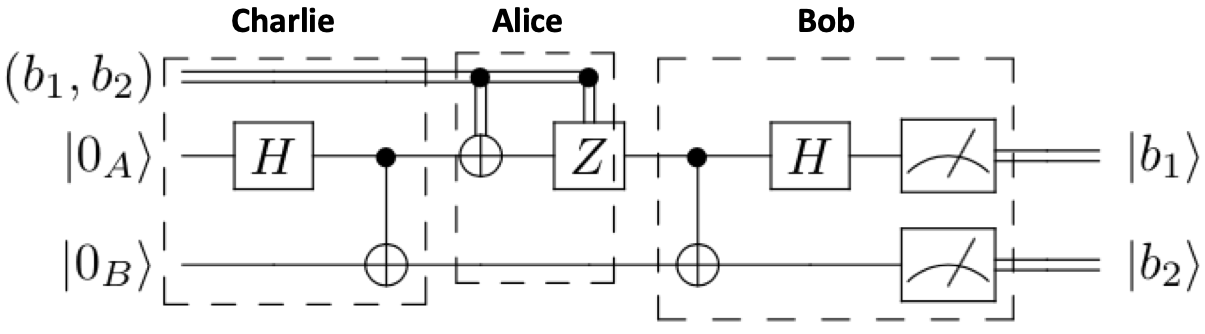
Steps¶
1. Charlie creates a bell state pair using a Hadamard (\(\textbf{H}\)) and Controlled-Not (\(\textbf{CNOT}\)) gate, \(|AB\rangle = \frac{1}{\sqrt{2}}(|00\rangle + |11\rangle) \) to Alice and qubit \(B\) to Bob.
2. Alice operates on her qubit based on the classical bits she wants to send to Bob. If her first classical bit is a \(1\), she operates on her qubit with a \(\textbf{X}\) gate. If her second classical bit is a \(1\), she operates on her qubit with a \(\textbf{Z}\) gate. Then, she sends her qubit to Bob.
The 2-qubit quantum system, \(|\psi A B\rangle\), is in one of the four Bell States: \(\frac{1}{\sqrt{2}}(|00\rangle + |11\rangle)\), \(\frac{1}{\sqrt{2}}(|00\rangle - |11\rangle)\), \(\frac{1}{\sqrt{2}}(|10\rangle + |01\rangle)\), \(\frac{1}{\sqrt{2}}(|01\rangle - |10\rangle)\).
3. Bob returns to the computational basis by applying a Controlled-Not (\(\textbf{CNOT}\)) and a Hadamard (\(\textbf{H}\)) gate to the qubit from Charlie and Alice. Finally, Bob measures each qubit and now has both of Alice’s classical bits.
Tutorial¶
We will now implement superdense coding using netQuil’s framework of Agent and Connections to simulate sending of classical bits using a quantum network. The Devices module and Noise allows you to include realistic devices with noise in your quantum network.
Import Dependencies¶
from pyquil import Program
from pyquil.api import QVMConnection
from pyquil.gates import *
from netQuil import *
Setup Agents¶
Let us first define agent Charlie who creates and distributes the bell state pair to Alice and Bob. We can extend the agent classes and redefine our \(\textit{run()}\) methods. To create our bell state pair, we can use a Hadamard (\(\textbf{H}\)) and Controlled-Not (\(\textbf{CNOT}\)) gate from pyquil. Then, using netQuil, we want to distribute each qubit to Alice and Bob.
class Charlie(Agent):
'''
Charlie sends Bell pairs to Alice and Bob
'''
def run(self):
# Create Bell State Pair
p = self.program
p += H(0)
p += CNOT(0,1)
self.qsend(alice.name, [0])
self.qsend(bob.name, [1])
Now, we will create agent Alice. Alice will operate on her bell state pair from Charlie based on the classical bits she wishes to send to Bob and send her qubit to Bob. Bob will then convert back to the computational basis using a Controlled-Not (\(\textbf{CNOT}\)) and a Hadamard (\(\textbf{H}\)) gate. Finally, Bob will measure each qubit from Charlie and Alice to recreate Alice’s two classical bits.
class Alice(Agent):
'''
Alice sends Bob superdense-encoded classical bits
'''
def run(self):
p = self.program
qubitsCharlie = self.qrecv(charlie.name)
a = qubitsCharlie[0]
bit1 = self.cmem[0]
bit2 = self.cmem[1]
# Operate on Qubit depending on Classical Bit
if bit2 == 1: p += X(a)
if bit1 == 1: p += Z(a)
self.qsend(bob.name, [a])
class Bob(Agent):
'''
Bob reconstructs Alice's classical bits
'''
def run(self):
p = self.program
# Get Qubits from Alice and Charlie
qubitsAlice = self.qrecv(alice.name)
qubitsCharlie = self.qrecv(charlie.name)
a = qubitsAlice[0]
c = qubitsCharlie[0]
p += CNOT(a,c)
p += H(a)
p += MEASURE(a, ro[0])
p += MEASURE(c, ro[1])
Set up Program¶
We can now define our pyquil program to pass into each agent. We need to define read out bits for measurements from Eve and Bob.
program = Program()
# Create Classical Memory
ro = program.declare('ro', 'BIT', 2)
Simulate Network¶
Finally, we can define our agents, connect them, and simulate our program. For this demo, we will define Alice’s classical bits to be \([0, 1]\). Notice, that initially Charlie has qubits 0 and 1, in order to make the bell state pair, and Alice’s classical memory, \(\textit{cmem} = [0, 1]\).
# Define Agents
alice = Alice(program, cmem=[0,1])
bob = Bob(program)
charlie = Charlie(program, qubits=[0,1])
# Connect Agents
QConnect(alice, bob, charlie)
# Simulate Agents
Simulation(alice,charlie,bob).run()
qvm = QVMConnection()
results = qvm.run(program)
Check Results¶
We can check if Bob’s measurements match Alice’s intial classical bits. We can also print the wavefunction using pyquil’s WaveFunctionSimulator to see how our state collapsed.
from pyquil.api import WavefunctionSimulator,
def printWF(p):
'''
Prints the wavefunction from simulating a program p
'''
wf_sim = WavefunctionSimulator()
waveFunction = wf_sim.wavefunction(p)
print(waveFunction)
# Print Results
print('Alice\'s inital bits: ', alice.cmem)
print('Bob\'s results:', results)
printWF(p)
Extend Simulation¶
You have now created a program to simulate superdense coding! You are able to send two classical bits using only one quantum bit. It is now time to get creative. Add noise, add extra agents, or add more classical bits.